| |
Prendiamo in considerazione l’esempio di Einstein del treno .
Ammettiamo di essere alla presenza di un tratto
sufficientemente lungo di ferrovia in cui su due binari rettilinei e
paralleli si trovano due treni di uguale peso e di uguale lunghezza R=A-B di cui uno, di
colore rosso
è fermo alla stazione che si trova nel mezzo di questo tratto di linea ferroviaria e che potremo collegare ad un sistema
di riferimento in quiete, che chiamiamo S
corrispondente con il sistema di riferimento della banchina
ferroviaria, mentre un secondo treno, di
colore verde
, si trova in moto uniforme con una velocità vt
sul secondo binario ed a cui è collegato un sistema di riferimento che chiameremo
S'.
Ammettiamo che su entrambi i treni e sulla linea ferroviaria siano collocati dei regoli indicatori in modo tale che
un qualsiasi passeggero possa identificare la sua posizione rispetto al sistema di riferimento collegato con ciascun treno e rispetto a quello
collegato con la banchina ferroviaria.
Collochiamo appaiati in coda al treno verde
(mobile), un osservatore ed un passeggero che identifichiamo entrambi con un contrassegno
verde
, ed analogamente per il treno fermo, identificati questa volta con il
colore rosso.
Ammettiamo che i quattro individui siano tutti di uguale peso e muniti di
taccuino e di orologi di precisione perfettamente sincronizzati.
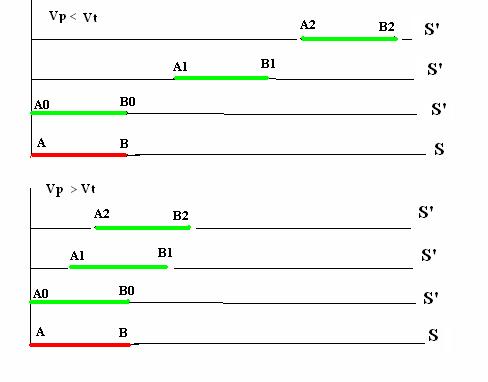
Nel momento in cui il treno verde si trova in coincidenza del treno rosso che
è fermo alla stazione, cioè quando il punto A della figura a lato (fig.1) corrisponde con il punto A i due passeggeri
alla coda di ciascun treno cominciano a muoversi di moto rettilineo
uniforme con velocità vp. Il nostro scopo è quello di determinare la legge del moto dei due passeggeri e dei treni nei due
sistemi di riferimento (S
ed S ) e la relazione tra i due sistemi stessi.
Consideriamo separatamente i dati registrati dall’osservatore rosso, che è sul treno fermo solidale con la banchina ferroviaria
e quelli raccolti dall’osservatore verde che si trova sul treno in movimento.
a) Moto
esaminato dall'osservatore rosso nel sistema S
in quiete rispetto alla banchina
L’ osservatore rosso
registra il tempo t0 in cui l’osservatore ed il
passeggero verdi in coda al treno che transita sul binario parallelo
sono con lui appaiati nel punto A ,cioè all’origine del sistema di assi cartesiani del treno fermo e della banchina.
In quell’istante il passeggero rosso ed il passeggero verde
iniziano il loro cammino e procedendo entrambi alla stessa velocità vp raggiungeranno contemporaneamente la testa dei loro rispettivi treni.
A quel punto l’osservatore rosso registra il tempo tB1 e le posizioni A1 e B1 dell’ osservatore
e del
passeggero verdi nel sistema di riferimento S
solidale con il treno rosso e con la banchina ferroviaria.
La velocità dei due passeggeri vp si determina dividendo lo spazio R, che corrisponde alla lunghezza del treno,
percorso dai due passeggeri nel rispettivo sistema di riferimento per il tempo t trascorso tra il momento della partenza tA0=tA
e quello dell’arrivo tB1.
vp= R/t
La velocità del treno vt si determina dividendo lo spazio percorso nel sistema di riferimento
S dall’ osservatore verde
seduto alla coda del treno per il tempo trascorso t.
vt=R(A1-A0)/t
Poiché la rilevazione delle distanze R(A1-A0), R(B1-A0), R(A-B) avviene al tempo t
che è sempre lo stesso ne conseguenza che la velocità del passeggero verde rispetto al sistema
S
sarà data dalla somma vt+vp quindi
v(tot) = vt + vp.
Possiamo quindi trovare la relazione tra le distanze percorse dai due passeggeri nei due sistemi di riferimento, infatti la distanza percorsa dal passeggero verde sarà
R(tot) = t * v(tot) = t(vt+vp).
Possiamo scrivere t = R/vp per cui
R(tot) = R(vt + vp)/vp= R(1+vt/vp).
Questa è la relazione che collega le distanze nei due sistemi di riferimento in moto tra di loro di un moto traslazionale rettilineo uniforme.
Se il passeggero verde dalla testa del treno in movimento ritorna in coda con la stessa velocità di spostamento vp
rispetto al sistema S',la sua velocità totale rispetto ad S
sarà (vt - vp) per cui arriverà al punto A2 avendo percorso una distanza totale
RA2B1=t(vt-vp)=(R/vp)(vt-vp)
=R(vt-vp)/vp= - R(vp-vt)/vp= - R(1-vt/vp).
Come si può vedere le due formule sono perfettamente equivalenti e si possono esprimere con una unica notazione se consideriamo il fatto che
nello spostamento del passeggero dalla coda alla testa del treno, la sua velocità è positiva e concorde con quella del treno mentre nello
spostamento del passeggero dalla testa del treno alla sua coda la sua velocità è negativa e discorde con quella del treno stesso.
Possiamo quindi scrivere che nel sistema di riferimento S la distanza percorsa
dal passeggero sul treno in movimento è data da
R'BA = R α con α = (1 ± vt/vp).
In cui R è la lunghezza del treno mentre R'BA è la lunghezza del treno più la distanza percorsa dal passeggero.
Per semplicità espositiva manteniamo separati il caso in cui gli spostamenti del treno e dei passeggeri sono concordi in cui possiamo scrivere
R'BA = R α+
con α+ = (1 + vt/vp).
da quello in cui essi sono discordi in cui abbiamo
R'BA = R α-
con α- = (1 - vt/vp).
Nella figura precedente (fig.1) sono esposti i due casi dove la velocità del passeggero vp è minore o maggiore di quella del treno vt.
xBA = x' α+ con
α+ = (1 + vt/vp). quando vp è positiva (eq. 1)
xBA = -x' α-. con
α- = (1 - vt/vp). quando vp è negativa (eq. 2)
b)
Moto esaminato dall'osservatore verde nel sistema S'
in moto rispetto alla banchina
Prendiamo ora in considerazione lo stesso processo visto dall’osservatore verde, solidale con il treno in movimento,
cioè collocato alla coda del treno che viaggia ed osserviamo come si scrivono le equazione nel suo sistema di riferimento
S'.
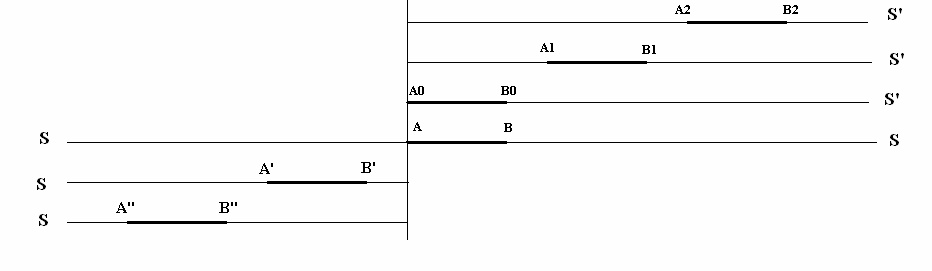
Il viaggiatore sul treno mobile raggiunge la testa del treno dopo un tempo t'=R/vp
Nel frattempo l’osservatore verde in A0 vede il treno rosso in S allontanarsi alla velocità
-vt ed il viaggiatore rosso in esso allontanarsi ad una velocità -vt+vp
pertanto lo spazio percorso dal viaggiatore rosso misurato dal sistema S' sarà dato da
R'A'B' = t'(-vt+vp) = (R/vp)(-vt+vp)
= - R (1 - vt/vp) =
= - R α- con α- = (1 - vt/vp).
Nel tragitto che va da B'' ad A'' la velocità del treno rosso rimane negativa mentre anche la velocità del passeggero rosso diventa negativa,
per cui avremo che il tempo rimane t = R/vp mentre la velocità totale sarà –(vt+vp). Per cui
R'A'B'' = -(R/vp)(vt+vp) = - Rα+ .
Anche in questo caso, cioè per il moto osservato dal sistema S',
possiamo generalizzare e dire che la coordinata x' ( nel sistema di riferimento S')
del passeggero rosso è data da
x' = x α- con α- = (1- vt/vp) (eq. 3)
quando vt e vp sono di segno contrario cioè il treno rosso sembra allontanarsi dall’osservatore vede ed il passeggero rosso sembra avvicinarsi
x' = - x α+ con α+ = (1 + vt/vp) (eq. 4)
quando vt e vp sono concordi cioè sia il passeggero che l’osservatore rossi sembrano allontanarsi dall’osservatore verde
L’esempio che abbiamo fatto mostra che la meccanica classica adotta in pieno il metodo riduzionistico introdotto da Cartesio e da Galileo nella
ricerca scientifica, riesce infatti a separare il fenomeno fisico “moto del passeggero” dal fenomeno fisico “moto del treno” per cui il fenomeno
fisico “ moto del passeggero” soddisfa il principio di relatività galileiano ed è indipendente dal sistema di riferimento adottato.
Infatti il passeggero verde si muove nel sistema S' con la stessa legge (x'= vpt)
con cui si muove il passeggero rosso nel sistema di riferimento S (x = vpt).
Il fenomeno fisico globale cioè “ moto del passeggero + treno” viene descritto combinando la legge del moto del passeggero (x = vpt)
che è invariante rispetto al sistema di coordinate con la legge che esprime la correlazione tra i due sistemi di riferimento che in genere è indipendente
dal sistema di riferimento che scegliamo per esprimerla, infatti abbiamo che nel sistema S
x = x' α+
con α+ = (1 + vt/vp) (eq. 1a).
mentre nel sistema S' abbiamo
x' = x α-
con α- = (1 - vt/vp ) (eq. 3a).
cioè nel sistema S la velocità globale ( passeggero + treno) si esprime come la soma algebrica delle due velocità parziali
vglob = vp +vt
Secondo la meccanica galileiana nei due sistemi di riferimento vale la stessa formulazione delle leggi del moto per cui la velocità
del treno vt e la velocità del passeggero vp si sommano ( o si sottraggono).
Queste leggi sono la diretta conseguenza del principio di conservazione dell’energia cinetica (od anche dell’impulso),
infatti a ciascun passeggero in movimento è associata una energia cinetica che è determinata dalla sua massa e dalla sua velocità di spostamento
generata dal lavoro muscolare, inoltre a quello dei due che si trova sul treno in movimento a sua volta sarà associata
una ulteriore energia cinetica associata al movimento del treno per cui il passeggero che si sposta dalla coda alla testa del treno
mobile con una velocità vp rispetto al sistema di riferimento S'
si sposterà rispetto al sistema di riferimento S ad una velocità vp + vt
che è determinata dalla propria energia cinetica determinata dalle due velocità.
Il passeggero rosso avrà quindi una energia cinetica
Ec = ½ m vp2 .
Mentre il passeggero verde avrà una energia cinetica data da
E'c = ½ m (vp+vt)2 =
½ mvp2 +½ m vt2 + mvpvt
che può essere scritta come
E'c = ½ m (vp+vt)2 =
½ m vp2(1+vt/vp)2 = Ec α+2
Il principio di conservazione dell’energia impone che l’energia muscolare dei due passeggeri sui due treni si sommi all’energia che essi
possiedono quando sono fermi infatti l’energia cinetica è data dall’integrale del momento lineare e quindi è definita a meno
di una costante additiva ma come mostra la precedente equazione in termini energetici i due sistemi di riferimento non sono equivalenti
perché ciascuno di essi ha una propria energia intrinseca come vedremo dopo esaminando l’effetto doppler.
A causa del principio di conservazione dell’energia quindi i due sistemi di riferimento, che sono equivalenti nel descrivere
il “ moto del passeggero” non lo sono quando dobbiamo descrivere il moto del “ passeggero + treno".
|
|