Relat05

	*Effetto Doppler Acustico*

	Lo studio dell’effetto Doppler acustico da la possibilità non solo di falsificare la teoria della relatività ma anche di fornire una spiegazione alternativa alla costanza della velocità della radiazione elettromagnetica e di integrare la formulazione della meccanica classica con la meccanica quantistica. Come è noto l’effetto Doppler acustico è costituito dalla variazione della frequenza del suono che si osserva quando un emettitore di suoni E è in movimento rispetto ad un ricevitore R. La formula generale è data da ν_R = ν_E (v_S + v_M - v_R )/(v_S + v_M - v_E) (eq. 11) In cui ν_R è la frequenza misurata dal rivelatore ν_E è la frequenza emessa, v_S = velocità del suono , v_M = velocità del mezzo in cui il suono si propaga, v_R = velocità del rivelatore v_E = velocità dell’ emettitore. Se invece della frequenza prendiamo in considerazione il periodo sapendo che ν_S = 1/τ_S abbiamo τ_R = τ_E (v_S + v_M - v_E )/(v_S + v_M - v_R) Un aspetto interessante di queste formule è che esse sono diverse a seconda che noi poniamo v_R= 0 oppure v_E = 0 cioè a seconda che sia in movimento l’emettitore od il rivelatore. In altre parole la frequenza osservata dipende dal fatto che l’osservatore sia in quiete od in movimento. Ammettiamo di essere nelle condizioni in cui v_M = 0 cioè il mezzo in cui si propaga il suono ( ad esempio aria) sia stazionario, in questo caso se v_R= 0 (cioè rivelatore fermo) si ha τ_R = τ_E (v_S - v_E )/(v_S ) = τ_Eα_- con α_- = (1- v_E/v_S) cioè quando il segno di v_E è lo stesso di v_S ,cioè l’emettitore si avvicina, allora il periodo misurato dal rivelatore è minore di quello generato dall’emettitore e quindi la frequenza aumenta; se invece v_E e v_S sono di segno contrario, cioè l’emettitore si allontana allora τ_R aumenta e quindi ν_R diminuisce. Se v_E= 0, cioè l’emettitore è fermo, avremo la seguente relazione τ_R = τ_E [v_S /(v_S - v_R] = τ_E/α_- cioè quando il rivelatore si avvicina alla sorgente del suono, e quindi i segni di v_S e di v_R sono contrari allora il termine in parentesi quadra è minore di 1 e quindi diminuisce il periodo ed aumenta la frequenza, mentre se i segni delle due velocità sono concordi, e quindi il rivelatore si allontana dall’emettitore allora si ha una diminuzione della frequenza. La cosa interessante è che anche quando v_R e v_E sono uguali (ad esempio alla velocità del treno v_t per riallacciarci al nostro caso) l’aumento di frequenza osservata quando il rivelatore e l’emettitore si avvicinano è diverso nei due casi in cui il rivelatore è fermo in S oppure è in moto in S'. Infatti tenendo conto dei segni delle velocità nel processo di avvicinamento abbiamo τ^S'_R /τ^S_R = [v_S /(v_S + v_t] / [(v_S - v_t )/v_S ] = v_S² /(v_S - v_t)(v_S + v_t) da cui ν^S'_R / ν^S_R = [v_S + v_t)(v_S - v_t)]/ v_S² = ( α_- α₊ ) = 1/γ² cioè se noi poniamo lo stesso emettitore di frequenze acustiche sui due treni, la variazione di frequenza registrata sul rivelatore posto sul treno in movimento è minore della variazione registrata dal rivelatore fermo sulla banchina. Per ricavare l’eq. 11 precedente facciamo un esempio pratico collegato con il nostro solito esperimento dei due treni. Poniamo che l’osservatore in coda al treno verde in movimento alla velocità v_t = 50 m/s (180 Km/ora) abbia un revolver capace di esplodere proiettili alla velocità v_p = 200 m/s, e che un revolver del tutto simile sia posseduto dall’osservatore rosso alla coda del treno fermo sulla banchina. Noi sappiamo inoltre che la velocità del suono in aria circa v_S = 344 m/s mentre la velocità della luce è 3 10⁸ m/s .Visto che l’ordine di grandezza della velocità della luce è molto maggiore di quello delle velocità che stiamo considerando, possiamo benissimo utilizzare la luce come elemento di sincronizzazione con un elevatissimo grado di approssimazione. L’osservatore rosso, fermo alla stazione, sta aspettando il treno verde che giunge da sinistra con velocità costante. [assegniamo un valore negativo alla coordinata che si trova alla sinistra dell’osservatore rosso ed un valore positivo alle velocità degli oggetti che si muovono verso destra] a-Moto del proiettile. Quando l’osservatore verde si trova alla distanza d₁ = -5.000 m dalla stazione esplode un colpo di pistola nella direzione dell’osservatore rosso che vede il lampo provocato dall’esplosione ed esplode a sua volta un proiettile nella direzione dell’osservatore verde. Secondo le leggi della meccanica classica avremo quindi la seguente situazione: t1_S = tempo impiegato dal suono relativo all’esplosione del proiettile verde per arrivare all’osservatore rosso t1_P = tempo impiegato dal proiettile verde per giungere all’osservatore rosso t1_t = tempo impiegato dal treno verde per giungere all’osservatore rosso per quanto riguarda l’osservatore in S' che è all’origine del suo sistema di coordinate d1 = x_finale – x _iniziale quindi x ha un valore negativo come pure negative sono le velocità degli oggetti che si muovono da destra verso sinistra t'1_S < t1_S poiché la velocità del suono rimane la stessa ma nel frattempo l'osservtore verde si avvicina all'osservatore rosso alla velocità v_t Come era da aspettarsi quindi le leggi della meccanica classica, nei due sistemi di riferimento sono invarianti per quanto riguarda i proiettili ed i treni ma non per quello che riguarda la velocità del suono. Possiamo vedere che il secondo proiettile verde arriva dopo 19 + 5 = 24 sec. mentre il terzo dopo 18 + 10 = 28 secondi e lo stesso per il proiettile sparato daltreno rosso. Ne consegue che un periodo di emissione di 5 secondi è pecepito come un ritardo di 4 secondi. b-Moto del suono Per quanto riguarda il suono invece l’osservatore rosso in S ode i colpi distanti di un tempo τ_R=Δt =13,808 +5 - 14.535 = 4.273 sec = 5•(1- v_t/v_S)= τ_E α_- e quindi ν_R = ν_E /α_- mentre per l’osservatore verde sul treno mobile in S' (per il quale il suono si propaga nel verso opposto a quello del treno) τ'_R =Δt'=12,056 +5 – 12.690 = 4.365 sec = 5/(1+ v_t/v_S)= τ_E /α₊ cioè ν'_R =ν_E α₊ Quando il treno verde sorpassa il treno rosso e continua la sua corsa verso destra avremo che per l’osservatore rosso il proiettile ed il suono che provengono da destra hanno un valore negativo della velocità il cui segno è quindi contrario a quello della velocità del treno che procede invece nello stesso verso per cui avremo τ_R = τ_E α₊ ed anche τ'_R = τ_E/ α_- perché per l’osservatore sul treno mobile che si trova alla destra dell’osservatore rosso il suono proveniente dalla banchina ed il treno si muovono nello stesso verso. Abbiamo ricavato quindi le formule, già note, che esprimono la variazione di frequenza per l’effetto Doppler acustico, ed abbiamo anche ritrovato il fattore di normalizzazione γ che Einstein aveva assunto implicitamente utilizzando le trasformazioni di Lorentz. Riassumendo quindi abbiamo il seguente schema per l’effetto Doppler classico Formula generale ν_o = ν_s (v + v_m - v_o )/(v + v_m - v_s) ν_o = frequenza osservata ν_s = frequenza emessa v = velocità del suono v_o = velocità dell'osservatore v_s = velocità della sorgente Le velocità sono positive se nella direzione in cui si propaga l’onda. Ipotizzando che v_m è zero, si possono verificare quattro casi: Cerchiamo a questo punto di capire la ragione di questa asimmetria di comportamento (in funzione del sistema di riferimento) che abbiamo trovato per l’effetto Doppler acustico. 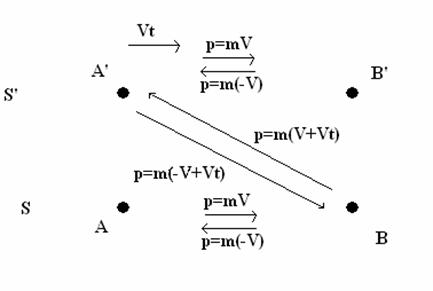Il principio di conservazione dell'energia e l'effetto Doppler acustico Prendiamo in considerazione il seguente schema: Vogliamo dimostrare che le leggi che governano l’effetto Doppler acustico, così come quelle che definiscono la meccanica classica sono una diretta conseguenza del principio di conservazione dell’energia. Ammettiamo che nei quattro punti sopra evidenziati, due sul treno rosso in quiete e due sul treno verde in movimento, vi siano quattro dispositivi identici, che indicheremo con la sigla (E/R) ,capaci ciascuno di emettere una frequenza sonora n_E uguale nei quattro emettitori e capaci di misurare le frequenze emesse dagli altri . Il meccanismo di trasmissione del suono in un mezzo consiste in un processo di trasmissione di energia, in cui non vi è trasporto di materia, attraverso un processo di urti elastici in cui le molecole del mezzo ricevono energia da una membrana acustica vibrante e la trasferiscono alle molecole circostanti. Il momento trasportato da una molecola adiacente alla membrana acustica è dato da p = mV in cui m è la massa della molecola e V è la velocità della membrana nella direzione della propagazione del suono. Vediamo dunque quale è la situazione che si determina nei quattro apparati (E/R). L’emettitore nel punto A trasmette un impulso con un momento p_E= mV nella direzione del punto B, se gli urti sono elastici come abbiamo ipotizzato, cioè in mancanza di perturbazioni esterne, il ricevitore nel punto B riceverà lo stesso impulso p_A= mV dopo un certo tempo e con la stessa frequenza con cui è stato emesso poiché la velocità di trasmissione del mezzo non cambia, ed il cammino che deve percorrere l’impulso è sempre lo stesso. L’energia trasferita nell’unità di tempo sarà data dall’energia di ogni impulso moltiplicato il numero di impulsi nell’unità di tempo cioè moltiplicato la frequenza cioè E = p•ν [ integrale ] Se il segnale acustico registrato in B proviene dall’emettitore in A' allora il momento trasferito dalla membrana vibrante in A' alle molecole del mezzo circostante sarà dato dalla somma del momento relativo all’apparato p=mV più quello relativo al moto dell’emettitore (momento intrinseco al sistema di riferimento) rispetto al ricevitore p_t=mV_t sarà quindi p_A' = m(V +V_t) , per cui essendo m= p_A/V si ha p_A' = p_A(V +V_t)/ V Se il segnale emesso in A' è ricevuto nel punto B' da un detector con un momento intrinseco uguale a quello dell’emettitore e cioè p_t=mV_t allora il momento trasferito sarà analogo a quello misurato nel sistema S e cioè p= m(V +V_t) - mV_t = mV. Poniamo a questo punto il rivelatore nel punto A' e misuriamo le frequenze dei suoni provenienti da B e da B', in questo caso abbiamo che il moto del suono ed il moto del treno sono diretti nel verso contrario per cui avremo per il suono proveniente da B' p_B' = -mV e per quello proveniente da B p_B= m(-V +V_t) per cui p_B'= p_BV/(V -V_t) in cui come abbiamo detto p_B' è il momento lineare degli impulsi sonori che arrivano in A' provenienti da B', mentre p_B è il momento degli impulsi sonori che arrivano in A provenienti da B. La frequenza di questi impulsi l’abbiamo calcolata precedentemente ed è data da (usando le stesse notazione) [ ν_R = ν_E / α_- ] ν_A' = ν_E / α_- = ν_E V/(V-V_t) è la frequenza degli impulsi che arrivano in B provenienti da A' mentre [ ν'_R = ν_E α₊ ] ν_B = ν_E α₊ = ν_E (V+V_t)/V è la frequenza degli impulsi che arrivano in A' provenienti da B. Come abbiamo detto l’energia trasportata nell’unità di tempo è data dall’energia di ogni impulso per il numero di impulsi nell’unità di tempo cioè E = p•ν per cui l’energia trasportata dal suono proveniente da A' che raggiunge B è E_A' = p_A' • ν_A' = p_A (V +V_t)/ V • ν_E V/(V -V_t) = p_A ν_E (V +V_t)/(V -V_t) Mentre quella che raggiunge A' proveniente da B è E_B' = p_B' • ν_B'= p_B V/(V -V_t) • νE(V +V_t)/V = p_B ν_E (V +V_t)/ (V -V_t) siccome p_A= p_B perché sono relativi alla frequenza ν_E dell’emettitore ne consegue che le due energie sono uguali. Questa è una conseguenza molto importante che è implicita nel principio di conservazione dell’energia, in effetti il fenomeno fisico che stiamo osservando è lo stesso sia che stiamo guardando dal sistema S che dal sistema S' tuttavia questo non vuol dire che la descrizione del fenomeno fisico, cioè le formule che utilizziamo siano le stesse in entrambi i sistemi di riferimento. Abbiamo quindi visto che è il prodotto p•ν invariante rispetto al cambiamento del sistema di riferimento mentre non lo sono i singoli termini p e ν . Le formule sono le stesse solo quando stiamo parlando del moto di corpi materiali in cui ( in particolare per sistemi di riferimento inerziale) perché in questo caso abbiamo la somma delle energie cinetiche, ma non quando parliamo di trasporto solo di energia come avviene per le onde acustiche o per le onde elettromagnetiche. Questa trattazione ha permesso di mettere in evidenza una considerazione molto importante e cioè che i sistemi inerziali sono equivalenti, anche per la trattazione dei fenomeni ondulatori solo quando il rivelatore e l’emettitore si trovano nello stato di moto o di quiete, cioè quando hanno la stessa energia cinetiche che chiameremo energia intrinseca al sistema di riferimento. La meccanica ha sempre assunto implicitamente che lo stato dell’osservatore sia del tutto indifferente ai fini della misura, e questo per raggiungere il criterio di oggettività; questa trattazione ha invece messo in evidenza che lo stato dell’osservatore, come avviene per la meccanica quantistica può influenzare il risultato della misura in funzione della sua energia intrinseca, questo non significa non obbedire al criterio di oggettività ma semplicemente di rendersi conto dell’influenza dell’osservatore senza ignorarne il peso come è stato finora ipotizzato spingendo inconsciamente Einstein verso la sua teoria della relatività. Abbiamo visto che il fattore g compare anche nella trattazione del fenomeno acustico e pertanto non è legato al valore elevatissimo della velocità della luce come derivato da Einstein, cade così anche l’altro simulacro che è stato utilizzato da Einstein per accreditare la sua teoria, e cioè che essendo la velocità della luce una velocità limite irrangiungibile , nessuno sarebbe stato in grado di falsificare la sua teoria. Introducendo il fattore di normalizzazione γ Einstein ha di fatto ignorato il peso che ha lo “stato” dell’osservatore nel determinare la misura del fenomeno fisico. Questo “stato” è alla base del principio di indeterminazione di Heisenberg che costituisce a sua volta un fondamento indispensabile per la meccanica quantistica. L’estensione di questo concetto anche alla meccanica classica permette di enunciare un vero e proprio “ principio antropometrico” che può essere così enunciato, “ per obbedire al criterio di oggettività, ogni fenomeno fisico deve essere indipendente dallo stato dell’osservatore, ma la rappresentazione matematica di tale fenomeno non può prescindere dallo 'stato' dell’osservatore che deve pertanto essere esplicitato nella fase di determinazione”. Il caso dei proiettili . Abbiamo visto che il prodotto E = p • ν è invariante quando prendiamo in considerazione il trasporto dell’energia acustica, vediamo ora cosa accade per il trasporto di oggetti dotati di massa, cioè consideriamo cosa accade per i proiettili che vengono esplosi dai due revolver nei treni del precedente esempio. L’osservatore rosso nel punto B vede arrivare i proiettili esplosi dal punto A con una frequenza ν _A mentre i proiettili esplosi dal punto A' che si sta avvicinando con velocità V_t arrivano con una frequenza ν_A' = ν_A(1+ V_t/ V_p) discorso analogo per quello che riguarda il momento dei proiettili che arrivano in B da A (p_A) e da A' (p_A' = p_A (1+ V_t/ V_p) per cui il prodotto sarà E = p_A' • ν_A' = p_A • ν_A(1+ V_t/ V_p)² che è la stessa relazione che lega l’energia cinetica del proiettile in A' con quella del proiettile in A e cioè Ec_A'= ½ m (V_p +V_p)² = ½ m V_p² (1+ V_t/ V_p)² = Ec_A (1+ V_t/ V_p)² Quindi l’energia cinetica ed il prodotto p • ν si trasformano nello stesso modo e sono quindi invarianti rispetto al cambiamento di coordinate in un sistema inerziale. Per quanto riguarda il momento p abbiamo ottenuto lo stesso risultato sia per quello che riguarda la membrana acustica che per quello che riguarda il proiettile, per quanto riguarda la frequenza ν invece abbiamo visto che per il proiettile ν_A' = ν_A (1+ V_t/ V_p) in cui ν_A è la frequenza di emissione dei proiettili, mentre per l’onda acustica ν_A' = ν_E /α_- = ν_E V/(V -V_t). la ragione di questo sta nel fatto che l’onda acustica non trasporta materia ma soltanto energia.