| |
La precedente trattazione ha mostrato che il principio di relatività della meccanica
classica e la costanza della velocità della luce, come corollario
dell’elettrodinamica, non sono conciliabili senza l’introduzione di nuovi
parametri e di nuovi concetti.
La meccanica quantistica da oggi la possibilità di affrontare il problema in modo
appropriato, ciò che non era possibile al tempo della pubblicazione del
primo lavoro di Einstein ma che sarebbe stato possibile successivamente se
Einstein non si fosse sempre rifiutato di considerare la quantomeccanica
come nuova frontiera della fisica.
L’operazione che fa Einstein per risolvere è semplicemente quella di imporre la costanza della velocità
della luce nei due sistemi di riferimento considerando la radiazione
elettromagnetica come un qualsiasi corpo materiale dotato di massa e di
energia cinetica.
Nel lavoro del 1905 infatti egli afferma:

Per fare questo utilizza le trasformazioni di
Lorentz che egli ricava in diversi modi nei vari lavori da lui pubblicati
nel corso degli anni.
Esse sono
x'= γ(x- vt t); t'= γ(t- xvt/vL2);
in cui γ2 =
1/ [(1- vt/vL) (1+ vt/vL)] =
1/[(1- vt2/vL2)]
se teniamo conto che nel sistema stazionario S vale la relazione x = vLt
possiamo trasferire l’espressione t = x/vL nella
prima e nella seconda relazione per cui
x'= γ x (1- vt/vL) t'= γ t (1- vt/vL)
con queste condizioni, cioè introducendo il termine γ come fattore di normalizzazione tra i due sistemi di riferimento, i valori
della velocità della luce rimangono identicamente uguali perché
x'/ t' = [γ x (1- vt/vL)]/[ γ t (1- vt/vL)] = x/t
ed inoltre la forma di γ assicura che per valori di vt molto minori di vL
ritornano valide le trasformazioni galileiane.
Naturalmente rinormalizzare i sistemi di riferimento in modo da mantenere costante la velocità della
luce all’interno di una trattazione classica della radiazione
elettromagnetica comporta una ridefinizione dei valori e dei concetti di
spazio e tempo tali da vanificare ogni pretesa di conoscenza oggettiva su
cui la scienza ha basato la propria validità.
La generale accettazione da parte del mondo
scientifico della teoria della relatività è stata determinata in gran
parte dal fatto che la velocità della luce non è in pratica raggiungibile da parte di nessun corpo in
movimento se non da particelle elementari in grandi acceleratori e con enorme dispendio di energia, cioè
come abbiamo accennato la teoria non è falsificabile. Tuttavia vedremo che
la problematica che si presenta con la velocità della luce non ha niente a
che vedere con il valore che tale velocità assume e che non compare mai
nelle varie formule e si ripresenta anche per velocità molto minori che
rimangono costanti nei vari sistemi di riferimento, come ad esempio
nell’effetto Doppler acustico che vedremo nelle pagine seguenti.
In una delle diverse procedure che utilizza per
ricavare le trasformazioni di Lorentz Einstein equipara direttamente le
due espressioni che determinano la coordinata spaziale x nei due sistemi
di riferimento.
Se utilizziamo il nostro formalismo vediamo che sostituisce nell’espressione
x' = x α- (eq. 3) (in cui l'osservatore è in S )
il valore di x' ricavato dall’espressione x = x' α+ (eq. 1) per cui
xα- = x /α+ da cui 1 = 1/( α+ * α-)
=> 1 = 1/( 1- vt2/vL2) = γ2
che compare nelle trasformazioni di Lorentz in cui il
fattore di normalizzazione γ rimane automaticamente soddisfatto, cioè γ=1 quando vt
= 0 cioè quando il treno è fermo, evidenziando quindi una ulteriore
contraddizione all’interno della teoria che vuole analizzare sistemi di
riferimento in movimento relativo tra loro.
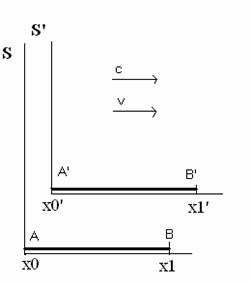
Se noi introduciamo questo fattore di normalizzazione nelle equazioni
della trattazione del nostro problema, cioè dell’impulso laser che viaggia
nei due treni analizzato da un osservatore sul sistema di riferimento in
quiete S allora
sapendo che nel sistema S possiamo sempre scrivere
x = vLt e quindi t= x/vL abbiamo
x'= γx(1- vt/vL) t'= γt(1- vt/vL)
per cui se esprimiamo le coordinate delle estremità del treno in movimento rispetto
al sistema S abbiamo
(x'B'-x'A') = γ(1- vt/vL)(xB-xA) =
γα- (xB-xA) (eq. 9)
da cui
(x'B'-x'A')/(xB-xA) = γ(1- vt/vL) =
[(vL- vt)/(vL+ vt)]1/2
cioè la differenza tra le due coppie di coordinate che rappresentano la
lunghezza del treno nei due sistemi di riferimento non sono uguali ,per
cui, come afferma Einstein, lo spazio nel sistema S' si accorcia rispetto
al sistema S.
Se poniamo l’osservatore nel sistema S'
per l’impulso laser che viaggia in S ; essendo in questo caso x'=vLt
avremo :
x = γ x'α+ per cui (xB-xA) = γ α+ (x'B'-x'A')
cioè
(x'B'-x'A') = (xB-xA)/[ γ α+ ] (eq. 10)
uguagliando (eq. 9) con (eq. 10) abbiamo
γ α- = 1/[ γ α+]
che rimane completamente soddisfatto dimostrando che le trasformazioni di Lorentz
soddisfano oltre la costanza della velocità della luce anche il principio
di relatività.
Le trasformazioni di Lorentz, attraverso un processo di rinormalizzazione,
soddisfano quindi pienamente il principio di relatività della meccanica
classica ed il principio della costanza della velocità della luce, ma
quello che si perde è il concetto fondamentale di osservabile che è la
base su cui si fonda la speculazione scientifica e cioè che la lunghezza
del treno non può dipendere dallo stato di quiete o di moto
dell’osservatore e del suo sistema di riferimento ( scienza soggettiva) .
La veridicità della scienza si basa quindi sulla oggettività del fenomeno
fisico pur ammettendo che vi possa essere una difformità della
rappresentazione matematica in funzione del sistema di riferimento
adottato ed il sistema di riferimento adottato per tale rappresentazione
viene spesso definito in funzione della semplicità matematica della
descrizione pur non inficiando la natura del fenomeno ( es. coordinate
sferiche ecc.)
Einstein nella sua teoria ha privilegiato una
uniformità formale piuttosto che sostanziale e per salvaguardare il
principio della costanza della velocità della luce, all’interno della
meccanica classica, ha sacrificato il significato fisico di spazio e di
tempo su cui si basa ogni concetto di velocità che di fatto è una
grandezza derivata e non una grandezza fondamentale.
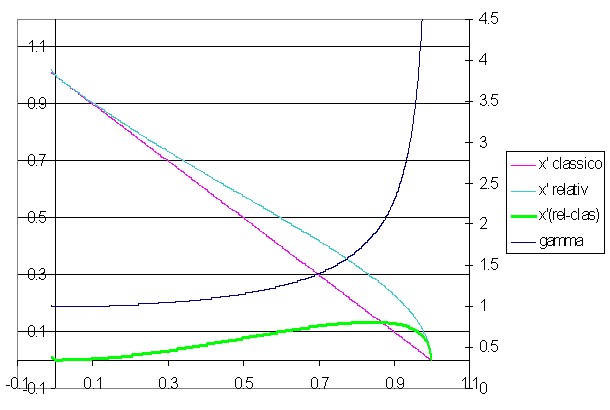
Una ulteriore incongruenza della teoria della relatività risulta dal plot
del valore di x' nel caso classico e nel caso relativistico nella figura in cui è riportato
anche il valore di di γ e (x'rel -x'clas) in funzione del rapporto v/vL .
Il valore classico è una linea retta che va da 1 a zero, nel caso in cui
la velocità v sia uguale a vL, questo significa
che se il treno viaggiasse alla velocità della luce allora l’impulso
laser ( cioè tutti i fotoni che lo costituiscono) sarebbero fermi rispetto
al treno. Questa è una situazione che pur sembrando paradossale si
verifica quando noi associamo un sistema di riferimento S' ad un impulso
laser ed andiamo ad analizzare le velocità dei fotoni costituenti e le
loro distanze relative. Se noi applichiamo le formule relativistiche ad
una tale situazione avremmo che la distanza dei vari fotoni all’interno
dell’impulso sarebbe infinita. Qualcuno potrebbe obbiettare che non vi è
la possibilità pratica di andare a verificare una tale situazione,
tuttavia la verifica può essere fatta al momento in cui l’impulso
interagisce con la materia che rimane ferma nel sistema di riferimento del
laboratorio per esempio facendo coincidere due impulsi laser su un
cristallo generatore di seconda armonica.
Quello che non è spiegabile poi è l’andamento del valori di x'
relativistico che all’inizio della curva diventa maggiore del classico (da notare che se x
aumenta significa che la velocità v diminuisce come visto
nell'esempio del treno in cui la velocità della luce sembrava diminuire)
per poi cambiare andamento per valori di v/vL=
0.839 e poi andare a valori negativi in vicinanza di 1.
E’ evidente che tale andamento non ha nessun significato fisico e le trasformazioni di Lorentz
si rivelano più un artifizio matematico che una legge fisica.
Nella precedente trattazione avevamo trovato che l’osservatore verde riceveva
l’impulso laser riflesso dallo specchio alla testa del treno mobile dopo
un tempo dato da
tA2A0 = tB1A0 + tA2B1=
(R/vL) α+ + (R/vL) α- = tBA α+ + tBA α- = 2 tBA
assumendo la velocità della luce come costante
universale e trattando il fotone come una semplice particella dotata di
massa e di energia cinetica, cioè applicando alla radiazione
elettromagnetica le stesse leggi della meccanica classica Einstein
perviene alle relazioni:
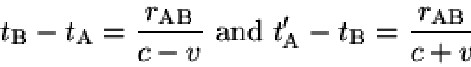
che espresse nei termini da noi utilizzati risultano
tB1A0 = R/(vL - vt) = [R/vL] [vL/( vL - vt] = tBA /α-
tA2B1 = R/(vL + vt) = [R/vL] [vL/( vL + vt = tBA /α+
per cui
tA2A0 = tB1A0 + tA2B1=
tBA [1/α- +1/α+] ) = tBA [(α- +α+)/(α- •α+)] = 2tBA γ2
per qualsiasi valore di vt diverso da zero si ha che il termine γ2>1
per cui si evidenzia una ulteriore contraddizione della teoria della
relatività ristretta che partendo dal postulato della costanza della
velocità della luce arriva alla conclusione che la luce per fare un percorso di
andata e ritorno sul treno in movimento impiega un tempo maggiore di
quello che essa impiega sul treno fermo sulla banchina.
Le equazioni della meccanica classica non sono quindi in grado di spiegare la
costanza della velocità della luce e la teoria della relatività ristretta
di Einstein attraverso le trasformazioni di Lorentz rendono conto della
costanza della velocità della luce ma stravolgono completamente i
fondamenti della meccanica classica. La considerazione che la velocità
della luce sia di fatto irrangiungibile ha minimizzato l’impatto di questa
teoria ha avuto sulla comunità scientifica.
In realtà il valore di vL non
è mai stato preso in considerazione nella teoria e la stessa problematica
si trova inalterata anche per velocità molto più basse, quali quelle
della trasmissione del suono.
|
|